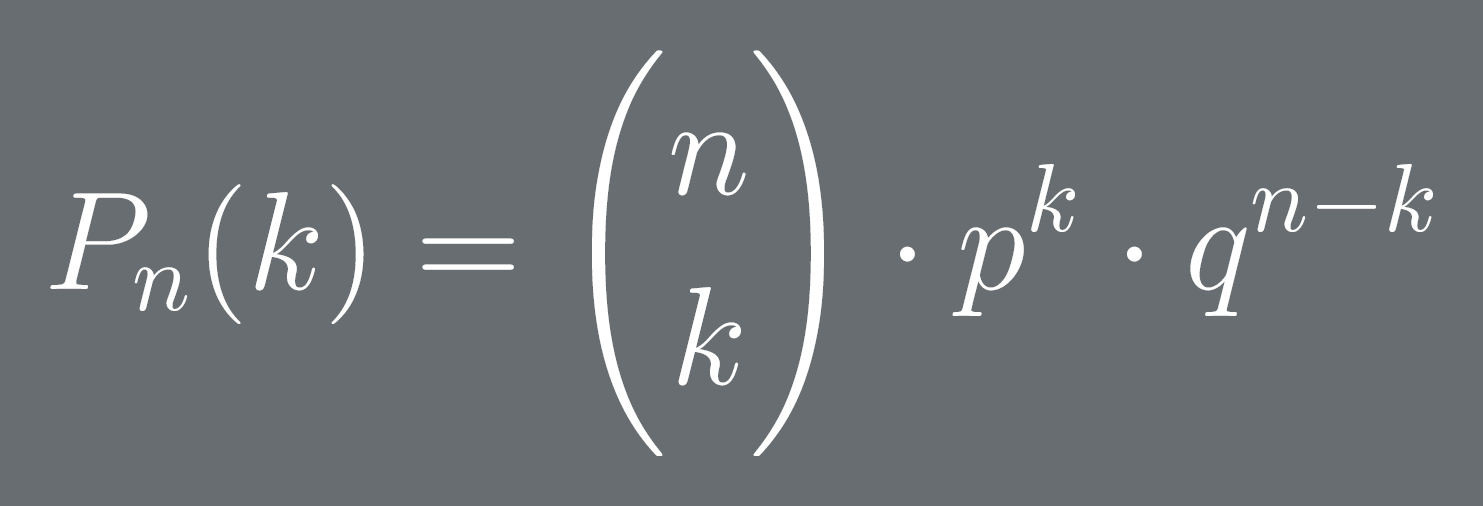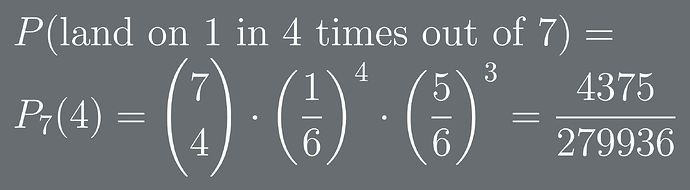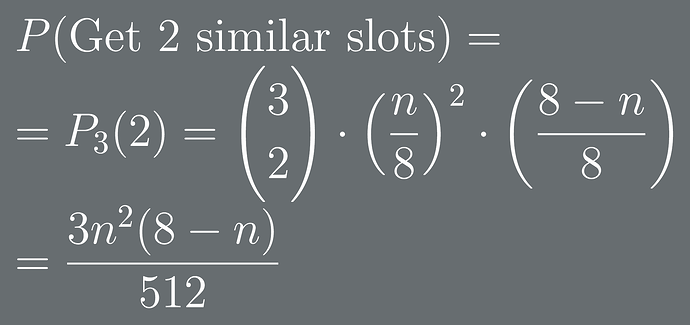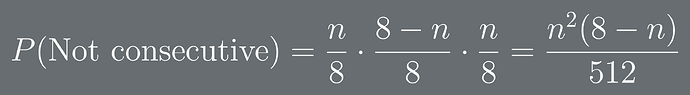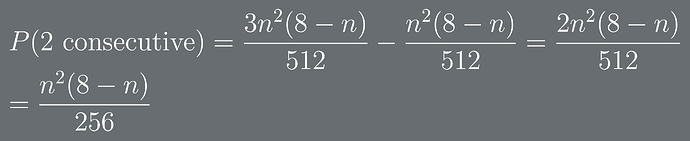Hub Lottery
A Mathematical Probability Analysis
Section #1 - Hub Lottery: An Introduction.
Introduction
The following thread is not quite the same as the common MunchyMC forums post.
This thread will show off an hour (it wasn’t that hard) of precise mathematical analysis of the Hub Lottery game, conducted by a Mathematics and Computer Science student.
For those reading that are unaware of the hub lottery game, the hub lottery game is a slot machine that can be played in the MunchyMC hub, as a reward for voting. The slot machine was coded to be entirely random and is meant to reward the player with respect to the results of the game.
The following analysis will mainly cover probability, however, it will also cover other discoveries made on the hub lottery using mathematics.
(so that i won’t be called a nerd in the replies, please know that while this thread is accurate, it was done for my own entertainment and as a joke. thx)
Rules
For those familiar with slot machines, the lottery follows the same rules.
There are 5 different options in each slot. Each slot rotates a random amount of times until eventually stopping on one of the options.
Once the three slots are in place, the player is to receive their reward (which will be mentioned below).
Rewards
The rewards for the lottery machine are as follows:
Gold Nugget: 5 tokens
Gold Ingot: 10 tokens
Golden Apple: 15 tokens
Emerald: 20 tokens
Diamond: 50 tokens
Discovery Explanation
Due to the rewards not being publicly available anywhere apart from this thread, I had to use algebra in order to construct a list of equations that would help me determine the value of each slot option.
Let the following parameters represent the following values:
x: Gold nugget
y: Gold ingot
z: Golden apple
α: Emerald
β: Diamond
After each round, the slots and the reward have been recorded.
All of the equations follow the same pattern:
(Sum of slot values) = (Reward) / (**If 3 consecutives**: 10, **Otherwise**: 1)
If we were to get 3 consecutive in a row, the reward would be multiplied by 10. Therefore, to calculate the value of the singular item, we would have to divide the reward by 10, and only then solve for the value of the remaining parameter.
Equations
Note: Each equation was built based on in-game lottery games, conducted by myself and @Simfonija
1) x + y + x = 2x + y = 20
2) x + y + β = 65
3) x + x + x = 3x = 150 / 10 = 15
**x = 5**
1) 2 * 5 + y = 20
10 + y = 20
**y = 10**
2) 5 + 10 + β = 65
15 + β = 65
**β = 50**
4) z + x + z = 2z + x = 35
2z + 5 = 35
2z = 30
**z = 15**
5) β + α + x = 75
50 + α + 5 = 75
55 + α = 75
**α = 20**
In the case of 2 consecutive similar slots, the player would be rewarded 1.5x the reward of the regular slot’s value, for each of the consecutive slots.
For example, if a player were to land on nugget - ingot - ingot, he would be rewarded 1.5x for each of the ingots, thus making it 5 + 10 * 1.5 + 10 * 1.5 = 5 + 15 + 15 = 35
Discovery Explanation
While showing off my analysis to fellow scientist @glug4glug, he was playing the lottery when I noticed that as the reward for getting the combination: diamond - nugget - nugget, he got 64 tokens instead of the expected 60.
After running a few more tests, I noticed that the same happened for gold - gold - emerald, where I was rewarded with 50 tokens instead of the expected 40 (We got an extra 10 tokens, which are double the amount of half the value of gold in the slot machine).
Knowing the value of each option beforehand, we deducted that two consecutive slots give you 1.5x the regular value for each consecutive slot.
We also remembered that we got 64 tokens instead of 60 the first time this occurred, which is an extra 4 tokens from the expected value, which is half the regular value of a nugget in the slot machine if rounded down to 2. Thus, we deduced that the prize for each of the two consecutive slots is (floor(1.5v)), where v is the regular value of the slot.
In the case of 3 consecutive slots, the player would be rewarded 10x the reward for the sum of the three slots.
For example, If a player were to get 3 consecutive emeralds, he would be rewarded 600 tokens ((20 * 3) * 10 = 600).
Discovery Explanation
This is public information. Upon winning 3 consecutive slots in a row, a message is broadcasted letting everyone in the lobby know that the player was rewarded 10x the regular slots prize.
Section #2 - Probabilities
An Introduction to Probability
So that I won’t have to repeat myself throughout this section, I thought I should go over some basic concepts in probability.
We represent probability using P(event).
The most basic probability formula is the number of times our desired outcome appears, out of the total number of outcomes that exist. For example, let’s say we want to roll a regular die and land on 4. The number 4 appears once on the die and there are 6 numbers on a regular die, therefore P(landing on a 4) = 1/6. Therefore, in theory, we should land on a 4 once every six throws. If, for example, we wanted to land on an even number, then there are 3 even numbers on a regular die, therefore P(even number) = 3/6 = 1/2. Therefore, in theory, we should land on an even number three times every six throws, or once every two throws.
The next thing we should know is the meanings of and / or in probability. If let’s say, we wanted to know the probability of landing on an even number first and then on an odd number (in that exact order), we would multiply the two probabilities together. The probability of getting an even number is the same as the probability of getting an odd number, which is 1/2, therefore P(even then odd) = 1/2 * 1/2 = 1/4. Therefore, once every four attempts we will get this desired outcome. If let’s say, we wanted our die to land on either 1 or 6 in a singular throw of the die, we would add the probabilities together. The probability of getting 1 is the same as the probability of getting 6, which is 1/6, therefore P(1 or 6) = 1/6 + 1/6 = 2/6 = 1/3. Therefore, once every three attempts we will land on either 1 or a 6.
Finally, I’d like to present the Bernoulli formula for probability. The Bernoulli formula is meant to help find the probability of an event happening an exact amount of times out of a certain amount of attempts.
The Bernoulli Formula
Let n be the number of attempts.
Let k be the number of times the event should happen.
Let p be the probability of the event.
Let q = 1 - p
Example
If let’s say, we wanted to throw a die 7 different times and land on the number 1 in 4 of the 7 throws. Therefore, n = 7, k = 4, p = 1/6, q = 5/6.
Therefore, out of 279,936 attempts, the desired event would occur 4,375 times.
The Probability of Everything Hub Lottery
Starting from the bottom, the following ratios represent the probability of getting the different options in a singular slot.
P(Golden nugget) = 3/8
P(Golden ingot) = 2/8 = 1/4
P(Golden apple) = 1/8
P(Emerald) = 1/8
P(Diamond = 1/8
Going over to the second easiest probability to figure out, we have the probability of getting 3 of the same item in a row, those probabilities are as follows:
P(3 Golden nugget) = 27/512
P(3 Golden ingot) = 8/512 = 1/64
P(3 Golden apple) = P(3 Emerald) = P(3 Diamond) = 1/512
Explanation
Let p be the probability of getting a certain item in a slot, then we should find the probability for p happening 3 times, or in other words, p and p and p. As we learned earlier, that would be p * p * p which is also p^3.
Therefore, to find the probability of getting 3 in a row, we should cube the probability of getting a singular slot with this item.
Finally, the trickiest of them all would be to find the probability of getting two consecutive.
The probabilities of getting two consecutive slots are as follows:
P(2 Consecutive nuggets) = 45/256
P(2 Consecutive ingots) = 3/32
P(2 Consecutive apple/emerald/diamond) = 7/256
Explanation
To find the probability of two consecutive slots, we should first find the probability of getting 2 similar slots out of 3. For this, we’ll use the Bernoulli formula.
Let n be the number of times an item appears in each slot.
Now, we’ll find the probability of getting a different slot between two similar slots.
Then, we want the two similar slots to be consecutive, therefore, we’ll subtract the probability of there being a different slot between the two similar slots from the probability of getting 2 similar slots.
Therefore, to find the probability of getting two consecutive slots, we’ll substitute for n the number of times a certain item appears in each slot.
Section #3 - Confirming the Hypothesis
Simulating the Lottery
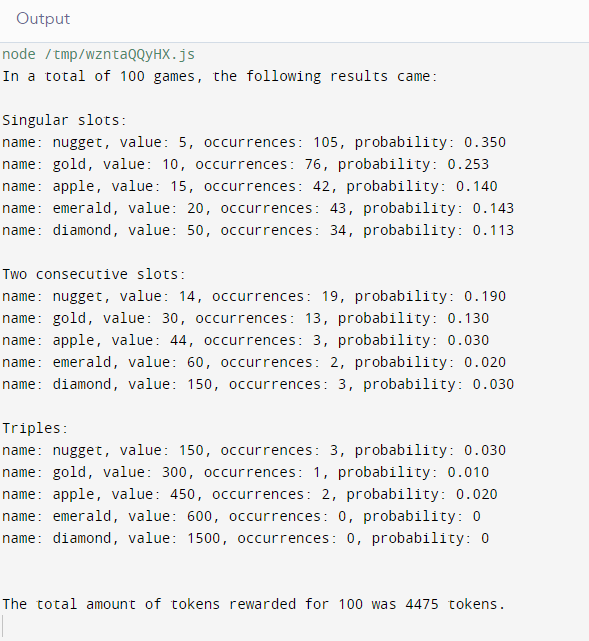
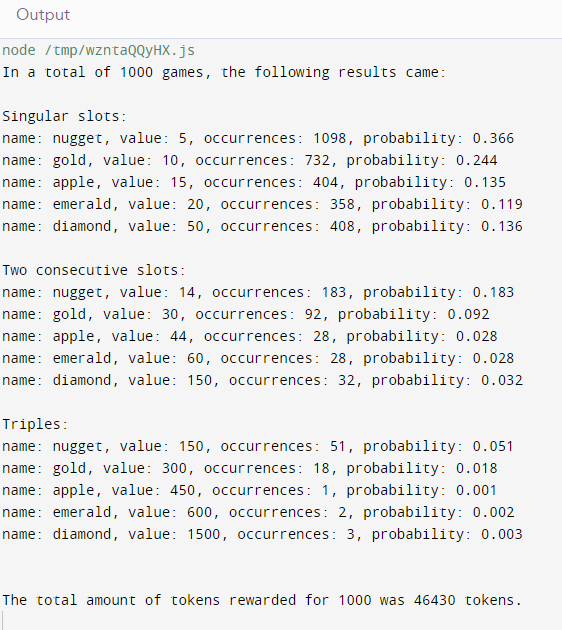
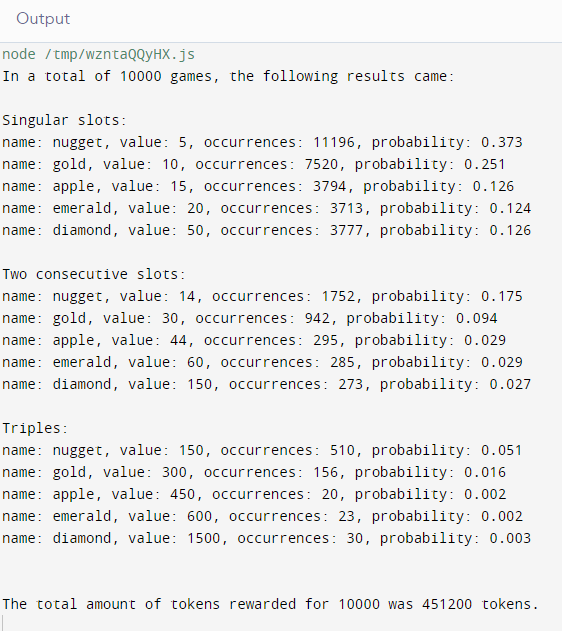
To confirm my hypothesis, I’ve coded a program to simulate the hub lottery.
I’ve run the program 5 times, each with a different number of games: 100, 1000, 10000, 100000, and 1000000:
As can be seen from the results of the program runs, the probabilities are very close to my hypothesis. We can also see that the probability of each event gets closer and closer to our hypothesis as we increase the number of games being run until it becomes the exact probability I calculated during the hypothesis stage.
If you’d like to run the program yourself, you can find the code here.
You can run the code in a JavaScript compiler of your choice. If you’re not familiar with compilers, you can use the one I chose for my analysis, found here.